§25. ТРИГОНОМЕТРИЧЕСКОЕ НИВЕЛИРОВАНИЕ
При тригонометрическом нивелировании определение превышения между двумя точками основывается на решении треугольника (рис. 113), катеты которого образованы направлением уровенной поверхности точки А и отвесной линией, проходящей через точку В, а гипотенуза — линией склона AB. Тригонометрическое нивелирование на местности включает измерение расстояния между точками А и В (мерной лентой или дальномером) и угла наклона α.
Угол наклона измеряется геодезическим прибором (вертикальным кругом
Прибор имеет также угломерное устройство с начальной линией отсчета, принимающей горизонтальное положение, т.е. параллельное отрезку AB уровенной поверхности.
Если склон направлен вверх от горизонтальной плоскости, то угол наклона и превышение положительные (со знаком плюс), вниз — отрицательные (минус).
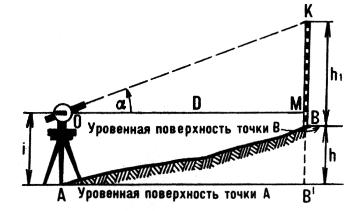
Рис. 113. Схема тригонометрического нивелирования
Для производства тригонометрического нивелирования в начальной точке А (рис. 113) устанавливают инструмент с вертикальным кругом; во второй точке В, высоту которой требуется определить,— рейку. Обозначим буквами: h — искомое превышение точек А и В, D — горизонтальную проекцию склона, i — высоту инструмента, КВ = l — высоту точки визирования на рейке. Из рисунка видно, что h+l = KM + i, отсюда h = KM+i — l. Из треугольника ОКМ: KM = D·tgα, следовательно, h = D·tgα+i—l.
Удобнее при измерении угла наклона (α) визировать на метку, закрепленную на рейке на высоте инструмента l = i, тогда при небольших углах наклона и расстоянии до 300 м используют сокращенную формулу: h = D·tgα.
Контроль точности определения превышений обеспечивается измерением прямого и обратного превышений и их равенством hобр. = –hпр.. Невязка в 3—4 см на 100 м расстояния считается допустимой.
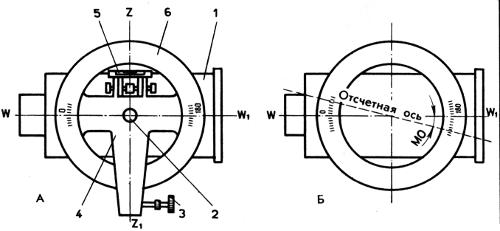
Рис. 114. Вертикальный круг теодолита (А). Место нуля вертикального круга (Б)
Углы наклона определяются при помощи вертикального круга теодолита и кипрегеля. В качестве примера рассмотрим принцип измерения вертикального угла α теодолитом (рис. 114). Вертикальный круг 6 теодолита вращается в вертикальной плоскости вокруг горизонтальной оси 2 вместе с визирной трубой 1, с которой он скреплен. С помощью неподвижной линейки — алидады 4 по ее горизонтальному диаметру, имеющему по обоим концам штрихи — нуль-пункты и верньеры, берут по вертикальному кругу теодолита отсчет величины угла наклона визирной оси трубы. Положение алидады фиксируется прикрепленным к ней цилиндрическим уровнем 5. Перед взятием отсчета пузырек уровня необходимо привести на середину с помощью наводящего винта 3. Естественно, что при горизонтальном положении визирной оси трубы и при среднем положении пузырька уровня алидады (совпадении диаметров 0—180° лимба и отсчетного устройства) в нуль-пункте отсчет по вертикальному кругу должен равняться нулю. Такой отсчет называется местом нуля (МО) (рис. 114).
Часто это условие (место нуля равно нулю) не сохраняется, в этом случае значение МО может быть определено при визировании одной и той же точки при двух положениях вертикального круга прибора — сначала справа и затем слева от наблюдателя. Полученные отсчеты соответственно обозначают КП и КЛ и место нуля определяют по формуле:
МО = (КП + КЛ+180°)/2.
Вычисление вертикального угла α для теодолита Т — 5 имеет вид α = МО – (КЛ + 180°) = КП – МО, а для Т — 30 α = КЛ – МО = = МО – (КП + 180°) или α = КП – КЛ , когда МО = 0.
Определение превышений кипрегелем или теодолитом заключается в измерении расстояния по дальномеру до дальномерной рейки, устанавливаемой в определяемой точке, и в измерении угла наклона по вертикальному кругу при КП, т.е. α = КП – МО. Далее по таблицам находят превышение h.
При рекогносцировочных геологических, ландшафтных и других полевых исследованиях для определения превышений точек (не требующих большой точности) применяют эклиметр. Расстояния при этом измеряют рулеткой или, что еще менее точно, шагами.
