3.2. НАХОЖДЕНИЕ ГЕНОТИПИЧЕСКИХ И АЛЛЕЛЬНЫХ ЧАСТОТ
Начнем с рассмотрения генотипических различий, контролируемых двумя аллелями одного аутосомного гена. Запишем схему моногибридного скрещивания и, ориентируясь на нее, введем понятие фенотипических и генотипических частот:
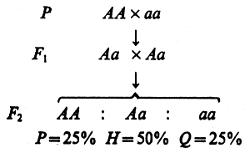
Пусть речь идет о наследовании различий в окраске цветков у ночной красавицы Mirabilis jalapa. Родительские формы обладают красной окраской (АА) и белой окраской (аа) цветков. Все дочернее потомство в F1, в соответствии с первым законом Менделя единообразно и характеризуется розовыми цветками, поскольку в данном случае имеет место неполное доминирование и промежуточное в сравнении с родителями выражение признака. Гибридные растения F1 дают женские и мужские гаметы двух типов: половина из них несет аллель А, тогда как другая половина — аллель а. При случайном комбинировании гамет в потомстве F2 будет иметь место расщепление на три фенотипических и соответственно генотипических класса — доминантных гомозигот, гетерозигот и рецессивных гомозигот. Ожидаемые частоты этих классов (обозначим их прописными латинскими буквами P, H, и Q) — 25, 50 и 25%. Таким образом, фенотипические и генотипические частоты в рассматриваемой ситуации (моногенные различия, неполное доминирование) есть доли особей трех указанных классов, выраженные в процентах или в долях единицы.
Экспериментатор при постановке моногибридного скрещивания задает генотипическую структуру потомства в дочерних поколениях и ожидает появления в F2 трех генотипических классов в соотношении 1:2:1. В природной популяции соотношение этих классов может варьировать в широких пределах. Его будут определять многие факторы, прежде всего относительная приспособительная ценность особей каждого класса, — их выживаемость, плодовитость, конкурентоспособность, а также система воспроизведения.
Представим себе природную популяцию ночной красавицы с растениями всех трех генотипов, идентифицируемых по фенотипу — окраске цветков. Как охарактеризовать ее по фенотипическим и генотипическим частотам? Для этого надо описать представительные (репрезентативные) выборки растений из популяции, т.е. подсчитать в каждой из них число особей с красными, розовыми и белыми цветками. Прежде чем суммировать данные отдельных выборок (дискретных распределений), надо убедиться в их однородности с помощью адекватного статистического критерия. Наиболее подходящим является критерий χ2. О правилах пользования им можно узнать из руководств по биометрии, указанных в списке литературы. Допустим, общее число растений в суммарной выборке составило 600. Из них 486 имело красные цветки, 108 — розовые и только 6 растений — белые. Принимая 600 за 100%, несложно рассчитать, что частоты трех фенотипических (генотипических) классов особей равны: P = 81%; H = 18%; Q = 1%.
Перейдем теперь к нахождению частот аллелей. В ситуации, когда анализируемые различия контролируются одной парой аллелей А и а, доминантные гомозиготы (АА) будут давать все свои гаметы с аллелью А, гетерозиготы (Аа) будут давать два типа гамет
А и а в равной пропорции и рецессивные гомозиготы (аа) — гаметы только одного типа а. Можно поставить вопрос о частоте появления гамет указанных двух типов в популяции в целом. Доли этих типов гамет как раз и будут соответствовать частотам аллелей. Они, так же как и генотипические частоты, выражаются в процентах или долях единицы и обозначаются строчными латинскими буквами p и q. Ясно, что значения частот аллелей определяются непосредственно из частот в популяции генотипических классов:
p = P + ½H; q = Q + ½H.
В табл. 3.1 представлены распределения генотипических частот в двух группах популяций.
Таблица 3.1. Распределение генотипических частот при моногенных различиях в двух группах популяций
| Группа популяций | |||||
|---|---|---|---|---|---|
| I | II | ||||
| P | H | Q | P | H | Q |
| 0 0,10 0,25 0,36 0,50 |
1 0,80 0,50 0,28 0 |
0 0,10 0,25 0,36 0,50 |
0,40 0,49 0,60 0,68 0,70 |
0,60 0,42 0,20 0,04 0 |
0 0,09 0,20 0,28 0,30 |
| p = q = 0,5 | p = 0,7; q=0,3 | ||||
Нетрудно видеть, пользуясь приведенными зависимостями между частотами аллелей и генотипическими частотами, что каждая из популяций группы I имеет значения p и q, равные 0,5, тогда как в каждой из популяций группы II p = 0,7; q = 0,3. Следовательно, одним и тем же значениям частот аллелей может в популяциях соответствовать, вообще говоря, бесконечное множество распределений частот генотипических классов. Однако существует условие, которое упорядочивает зависимость между генотипическими и аллельными частотами. Это условие заключается в случайном характере скрещиваний между особями в популяции. Популяции, где осуществляются свободные скрещивания, носят название панмиктических. Их нередко называют еще менделевскими, поскольку менделевские закономерности наследования находят в них свое выражение, чего не может быть в популяциях, воспроизводящихся каким-либо иным путем. Именно панмиктические, менделевские популяции привлекали наибольшее внимание генетиков-популяционистов, особенно тех, кто был занят разработкой теоретических вопросов статики и динамики генных частот.
Предыдущая | Оглавление | Следующая
