§21. ТЕОДОЛИТНАЯ СЪЕМКА
Плановая (горизонтальная) теодолитная съемка относится к угломерному виду съемок, при котором на местности измеряют расстояния лентой и дальномером и горизонтальные углы с помощью теодолита. Обычно применяется в равнинной местности для съемки населенных пунктов, застроенных участков и пр.
Горизонтальный угол β лежит в горизонтальной плоскости, его лучами служат горизонтальные проекции направлений на наблюдаемые объекты (рис. 69).
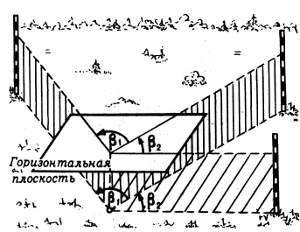
Рис. 69. Принцип измерения горизонтальных углов. Заштрихованы вертикальные плоскости, проходящие через точку установки инструмента (вершина измеряемого угла) и визируемые предметы
Применяемые приборы. Теодолит — геодезический инструмент для определения направлений и измерения горизонтальных и вертикальных углов при топографо-геодезических работах. Его основной рабочей частью служат горизонтальный и вертикальный круги с градусными и более мелкими делениями. Применяются приборы с металлическими и, главным образом, со стеклянными кругами. Последние снабжены оптическими отсчетными устройствами и называются оптическими теодолитами.
Современные теодолиты весьма разнообразны по конструкции, точности результатов измерений, массе. Однако основные узлы в разных теодолитах имеют много общего.
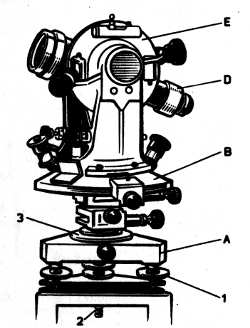
Рис. 70. Теодолит с металлическими кругами
Рассмотрим устройство одного из теодолитов, внешний вид которого показан на рисунке 70, а разрез дан на рисунке 71. Прибор, подобно другим геодезическим инструментам, устанавливается на штативе с помощью массивной подставки А, снабженной подъемными винтами 1 для приведения вертикальной оси инструмента в отвесное положение. Становой винт 2 соединяет подставку с треногой. Во втулку 3 входит ось вращения 4. Основные части теодолита: горизонтальный круг В с круговой шкалой-лимбом, алидадный круг С, зрительная труба D и вертикальный круг Е. Круг В служит для измерения горизонтальных углов, на его лимбе нанесены деления, цена которых 20' (рис. 72). Деления подписаны через 10° по ходу часовой стрелки от 0° до 350°. Ось горизонтального круга 4 может вращаться во втулке подставки 3. Ось алидадного круга 5 входит во втулку горизонтального круга В. Таким образом, оси вращения обоих кругов совпадают. На двух концах диаметра алидадного круга нанесена шкала для отсчитывания по лимбу, называемая верньером. Чтобы исключить при отсчетах влияние эксцентритета круга и алидады, среднюю величину отсчета вычисляют по парным отсчетам, взятым по обоим верньерам алидады.
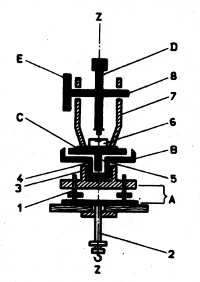
Рис. 71. Схема устройства теодолита
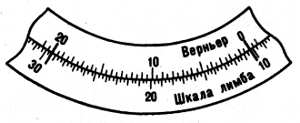
Рис. 72. Шкала верньера и часть лимба
Верньер служит для измерения углов с большей точностью, чем цена деления лимба1. Он представляет собой дугу, разделенную на равные части, число которых на единицу больше числа делений лимба, захватывающих ту же дугу. Следовательно, если обозначить цену деления лимба, выраженную в угловых мерах, буквой l, цену деления верньера (также в угловых мерах) — v, число этих делений лимба (n—1), а верньера — n, то можно составить равенство l(n—1) = vn или ln — l = vn; откуда ln — vn = l; n(l — v) = l. Обозначив (l — v) через t, назовем ее точностью верньера, получим: t = l/n.
Таким образом, точность верньера равна цене деления лимба, деленной на число делений верньера. Пользуясь этой формулой, определяют точность верньера теодолита. Если цена деления лимба 20' и на верньере 40 делений, то точность верньера t = 20'/40 = 0,5', т.е. t = 30".
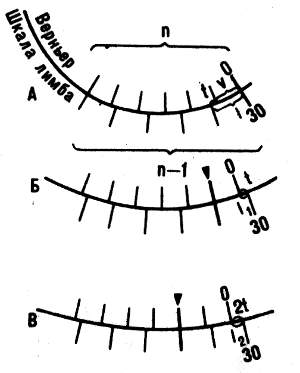
Рис. 73. Схема отсчета по верньеру: l — цена деления лимба; v — цена деления верньера; t — точность верньера, t=l — v. Совпадающие штрихи утолщены и отмечены треугольничком
Для отсчитывания по кругам данного теодолита используют лупы, а в оптических теодолитах — шкаловые микроскопы и оптические микрометры.
Полный отсчет по лимбу А складывается из отсчета А1, по основному кругу от 0 лимба до 0 верньера и отсчета по верньеру: A = A1 + a.
На рисунке 74 полный отсчет равен 53°33'30".
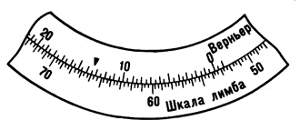
Рис. 74. Отсчет по лимбу и верньеру: 53°33'30''
Алидадный круг прикрыт кожухом, в котором над верньерами имеются окна. К кожуху прикреплены два цилиндрических уровня 6, с помощью которых лимб приводят в горизонтальное положение, а вертикальную ось инструмента — в отвесное. На рисунке 71 показан один уровень, так как второй не попал в плоскость чертежа.
К кожуху алидады крепятся подставки 7, поддерживающие ось вращения 8 зрительной трубы D и вертикального круга Е.

Рассмотрим по схематическому изображению верньера на рисунке 73, как производится отсчет с его помощью. На рисунке показаны участки дуг верньера и лимба в разных взаимных положениях. В первом случае (А) ноль верньера совпадает (сливается) со штрихом 30 на лимбе, следовательно, отсчет по лимбу равен 30°.
На втором рисунке (Б) показано, что ноль верньера сместился на дугу, равную одной точности верньера; при этом первый штрих верньера совпал (слился) с каким-то штрихом лимба.
Наконец, на нижнем рисунке (В) ноль верньера сместился на дугу, равную 2t, и при этом второй штрих верньера совпал с каким-то штрихом лимба. Отсюда следует, что для оценки величины дуги некоторой части одного деления лимба а надо найти номер штриха верньера n1, совпадающего с каким-то штрихом лимба, и умножить на точность верньера t, т.е. a = n1t.